스칼라, 벡터(Scalar, Vector)
스칼라는 방향은 없고 크기만 있고, 벡터는 크기와 방향 모두 있습니다.
예를 들어 →a=2→x+3→y 가 있다고 합시다.
여기서 벡터→a는 스칼라2와 단위벡터→x의 곱과 스칼라3과 단위벡터 →y의 곱을 더해준 벡터입니다.
벡터(vector)

벡터는 위의 그림처럼 알파벳 위에 화살표로 표현할 수 있습니다.
이 경우 왼쪽부터 2,3,1,4차원의 벡터입니다.
벡터의 크기 (Magnitude, Norm, Length)
벡터는 선이기 때문에 피타고라스 정리에 의하면
벡터의 크기는 모든 원소(스칼라)들의 제곱을 더해준 것에 루트를 씌운 것입니다.
표현은 ||으로 나타냅니다.
→b=[−4,7,1]
||→b||=√(−4)2+72+12
||→b||=√66
벡터의 크기는 다음과 같은 특징을 가집니다.
1. ||→x||≥0
2. 모든 원소(스칼라)가 0인 경우 ||→x||=0
3. 삼각 부등식 : ||→x+→y||≤||→x||+||→y||
벡터의 내적 ( Dot Product )
벡터의 내적은 두 벡터의 각 구성요소를 곱한 뒤 더해준 것입니다.
→a=[1,2,3]
→b=[4,5,6]
→a⋅→b=1⋅4+2⋅5+3⋅6
=32
벡터의 내적은 다음과 같은 특징을 가집니다.
1. 교환법칙 : →a⋅→b=→b⋅→a
2. 분배법칙 : →a⋅(→b+→c)=→a⋅→b+→a⋅→c
3. 두 벡터의 길이가 동일
매트릭스(Matrices)
매트릭스는 행과 열을 통해 배치되어있는 숫자들입니다.

매트릭스의 일치
2개의 매트릭스가 일치하기 위해서는 다음 조건을 만족해야 합니다.
1. 동일한 차원을 보유
2. 각 해당하는 구성요소들이 동일
Dimensionality(차원)
매트릭스의 행과 열의 숫자를 차원이라고 합니다.
예를들어 위의 Y행렬은 2x3차원이라고 합니다.
Matrix multiplication(행렬 곱)

Transpose(전치)
매트릭스의 전치는, 행과 열을 바꾸는 것을 의미합니다.
대각선 부분의 구성요소를 고정시키고 이를 기준으로 나머지 구성요소들을 뒤집는다라고 생각하면 됩니다.
이는 일반적으로 매트릭스 우측 상단에 T 혹은 tick 마크를 통해 표기 됩니다.
YTor Y′
Y=[123456]
YT=[142536]
정사각 매트릭스(square matrix)
행과 열의 개수가 같은 매트릭스입니다.

정사각 매트릭스에는 특별한 케이스가 있습니다.
1. Diagonal (대각): 대각선 부분에만 값이 있고, 나머지는 전부 0입니다.

2. Upper Triangular (상삼각): 대각선 위쪽 부분에만 값이 있고, 나머지는 전부 0입니다.

3. Lower Triangular (하삼각): upper triangular 와 반대로, 대각선 아래에만 값이 있습니다.

4. Symmetric (대칭): 대각선을 기준으로 위 아래의 값이 대칭인 경우 입니다.

5. Identity (단위 행렬): 대각선 부분이 1이고, 나머지는 전부 0입니다.
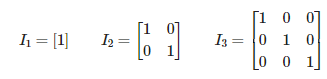
단위 행렬은 &I$로 표시하면 다음과 같은 특징이 있습니다.
1. 행렬A에 대하여 AI=A
2. 행렬A에 대하여 AA−1=I(A−1은 A의 역행렬)
Determinant(행렬식)
행렬식은 모든 정사각 매트릭스가 갖는 속성으로, $det(A)$ 혹은 $|A|$로 표기 됩니다.
A=[abcd]
det(A)=ad−bc
det는 역행렬을 구할 때 사용됩니다.
더 큰 차원의 매트릭스의 행렬식은 재귀적으로 부분을 이루는 행렬식을 구하는 것으로 계산 할 수 있습니다.
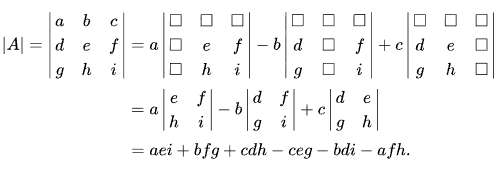
행렬식이 0이라면?
행렬식이 0인 정사각 매트릭스는 특이(singular) 매트릭스라고 불리기도 합니다.
이들은 2개의 행 혹은 열이 선형의 관계를 이루고 있을때 발생합니다.
또 다른 말로는,
매트릭스의 행과 열이 선형의 의존 관계가 있는 경우 매트릭스의 행렬식은 0이라고 할 수 있습니다.
Inverse(역행렬)
역행렬은 행렬의 역수와 같이 표현 할 수 있습니다.
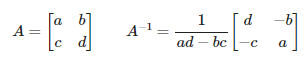
매트릭스에 그 역행렬을 곱하면 단위 행렬가 됩니다.
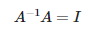
'채워가는 지식 > AI' 카테고리의 다른 글
| High dimensional data (0) | 2022.09.12 |
|---|---|
| 선형대수 2 (0) | 2022.09.08 |
| 베이지안 통계 개론 (Bayesian Inference) (0) | 2022.09.07 |
| Confidence Intervals (0) | 2022.09.07 |
| More Hypothesis Testing (0) | 2022.09.06 |